Short version: It looks like most mammals, at least most large mammals, have the brains they need, while primates, especially large primates, have the brains they can afford.
Longer version: One reason for being interested in monkeys is that they’re brainy mammals. Here’s the conventional graph illustrating that:
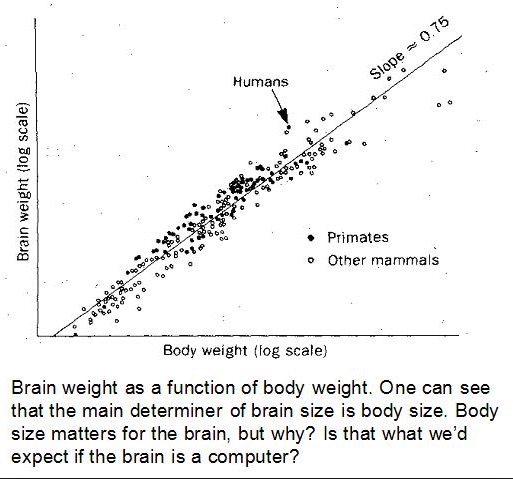
Larger mammals tend to have larger brains, but the relationship is non-linear. Multiplying body mass by x doesn’t multiply brain mass by x. Instead it multiplies brain mass by about x.75. In other words, Brain Mass is proportional to (Body Mass).75. Equivalently (taking the logarithm of both sides) Log[Brain Mass] is equal to .75 times Log[Body Mass], plus a constant. So Log[Brain Mass] plotted against Log[Body Mass] gives a straight line with a slope of .75. That means that if one mammal has 16 times the body mass of another, it’s expected to have 8 times the brain mass, 10,000 times the body mass means 1000 times the brain mass, and so on. The thing to note is that primates defy expectations. They have larger brains than would be expected based on their body sizes.
But we’ve recently learned that primates – especially big ones – are even more special than this graph suggests. Susan Herculano-Houzel has pioneered a technique that involves chopping up brains (or parts of brains), dissolving their cells to make a kind of brain soup, and counting cell nuclei. This allows her to estimate how many neurons there are in different brains.
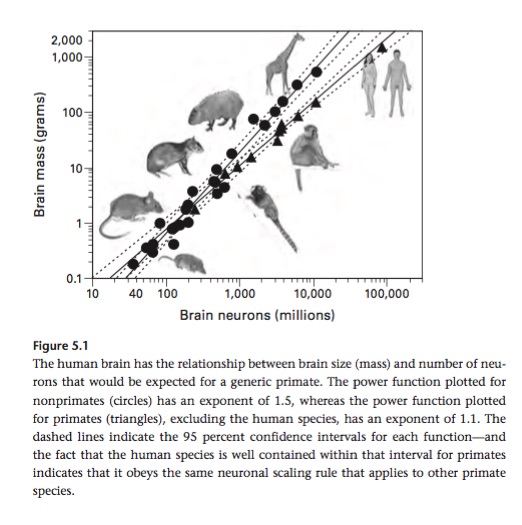
Major findings: Among most mammals, the number of neurons increases more slowly than brain size. Increase brain size by x, and you increase number of neurons by about x.67. (H-H shows this flipped around. Increase number of neurons by x and you increase brain mass by x1.5.) But primates are exceptional; the relationship is nearly linear. An x-fold increase in primate brain size corresponds to about an x-fold increase in number of neurons. Humans follow the primate rule here. We have about the same density of neurons as other primates. When you combine the exceptionally large brain sizes of humans (exceptional even relative to our brainy primate relations) with a standard high primate neuron density, you get an animal with an enormous number of neurons. By contrast, a rodent with a human sized brain, if it followed rodent rules for how neuron numbers increase with brain size, would have only 1/7 as many neurons.
Neurons are expensive. Most large animals economize by cutting back on neuron density. A cubic centimeter of cow brain has fewer neurons, and consumes energy at a lower rate, than a cubic centimeter of mouse brain (although of course the cow’s brain is bigger). By contrast, large primates are extravagant, devoting exceptionally large energy budgets to running their brains. And human brains are exceptionally costly. An important question for the study of human evolution is how we paid the bill for such costly brains. That’s a story for later. But another part of the story starts back in the early Cenozoic, when monkeys committed to a different set of rules for building brains.
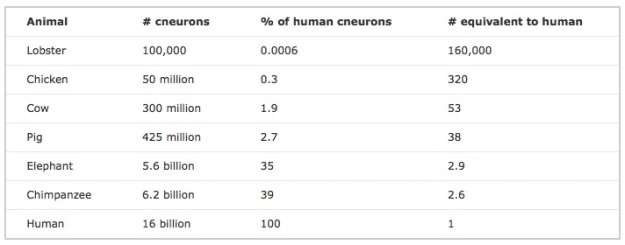
And here is a chart giving absolute numbers of cortical neurons (cneurons) for a bunch of species. Scott Alexander has some thoughts about the moral implications. Short version: skip the pork for dinner (and skip the elephant, chimp, and manflesh. But you knew that). Beef might be okay. Better is lobster.
And Werner Herzog is probably okay with you eating chicken.